Modulus of Elasticity of Concrete

Modulus of Elasticity

The modulus of elasticity or modulus of elasticity of concrete, often denoted as E or Elastic is a material property that describes the stiffness or rigidity of a material when subjected to deformation. In simpler terms, it measures how a material responds to an applied force by deforming or stretching. Mathematically, the modulus of elasticity is defined as the ratio of stress to strain within the elastic limit of the material.

The formula for the modulus of elasticity (E) is expressed as:

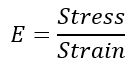
Here,

• E is the modulus of elasticity,
• Stress is the force applied to the material per unit area (e.g., in Pascals or Pounds per Square Inch),
• Strain is the resulting deformation or change in length relative to the original length.

The modulus of elasticity provides information about how a material will deform under a given amount of stress. A higher modulus of elasticity indicates a stiffer material that deforms less, while a lower modulus suggests a more flexible material that deforms more under the same stress.

Modulus of Elasticity of Concrete

The modulus of elasticity of concrete in compression is a property of concrete that represents the capacity of the material to resist deformation under applied load. The modulus of elasticity for concrete is characterized as the relationship between the applied stress expressed in N/mm² and the resulting strain mm/mm of gauge length. This is also known as elastic modulus, the coefficient of elasticity or sometimes known as Young’s modulus of elasticity for concrete.

It is the slope of the initial straight portion of the stress-strain curve. It is also termed as the initial modulus. It is a tangent at the origin. The modulus of elasticity varies with the strength. It is primarily influenced by the elastic properties of aggregate and to a lesser extent by the conditions of curing and the age of concrete, the mix proportions, type of cement, rate of loading and type and size of specimen.

Tangent Modulus of Elasticity of Concrete

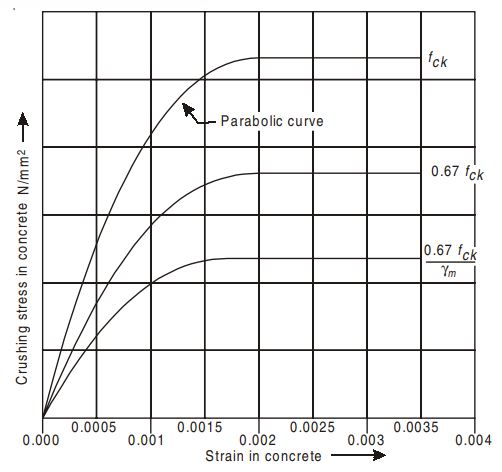
The tangent modulus of elasticity of concrete denoted by E_c, describes the total strain in concrete (including creep) and it is a variable quantity. In the below graph/figure (Design stress-strain diagram for concrete), it is defined as the slope of the curve at any given point.

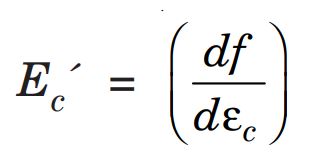
Here, df is a small increase in stress for a small increase in strain dε_c .

Secant Modulus of Elasticity of Concrete

Certain codes incorporate the concept of the secant modulus of elasticity, denoted as Ec’, in design calculations. This quantity represents the slope of the chord drawn through a point on the stress-strain curve corresponding to a specific stress. The secant modulus of elasticity is variable and generally smaller than the initial tangent modulus of elasticity.

When subjected to compression along one direction, concrete exhibits expansion in the direction transverse to the applied stress. The ratio of transverse strains to longitudinal strains is referred to as Poisson’s ratio. This ratio is influenced by factors such as strength, composition, and other considerations. For concrete under small stresses, the typical range for Poisson’s ratio is approximately 0.15 to 0.20.

Also, read: Poisson’s Ratio Of Concrete: Understanding Its Significance In Structural Behavior

Different Code for Modulus Of Elasticity Of Concrete

Various codes provide empirical relationships for calculating the Modulus of Elasticity of Concrete. The relationship has been derived between the modulus of elasticity (E or E_c) and compressive strength (√f_c​) of concrete. Here are a few of them.

According to ACI

According to ACI 318-08 section 8.5, the modulus of elasticity for concrete is:

1. For the value of w_c values between 90 and 160 lb/ft3 (1440 and 2560kg/m³).
   • Ec ​= w_c^1.5 X 33√f′c​​ in psi

2. For normal-weight concrete,
   • E_c​ = 57,000√f′c​​ in psi

Here, E_c​ is the modulus of elasticity in pounds per square inch (psi), and √f′c​ is the compressive strength of concrete in psi.

Also, read: Compressive Strength Of Concrete

According to BNBC

According to BNBC 2006 section 5.13.2.1,

1. For stone aggregate concrete,
   • When w_c between 15 and 25 kN/mm³ and √f′c in N/mm², E_c = 44w_c^1.5√f′c in N/mm²

2. For normal-density concrete
   • E_c = 4700√f′c in N/mm²

3. For brick aggregate concrete
   • E_c = 3750√f′c in N/mm²

Here, E_c​ is the modulus of elasticity in Newton per square millimetre (N/mm²), and √f′c​ is the compressive strength of concrete in N/mm².

According to the Indian Standard

According to the Indian standard 456-2000, the relationship between the modulus of elasticity (E) and compressive strength (√f_c​) of concrete can be expressed using the empirical formula as shown below:

E = 5000√f_c

Here, E​ is the short-term static modulus of elasticity in N/mm², and √f′c​ is the compressive strength of concrete in N/mm² of spacemen at various ages (usually, 7 days, 14 days and 28 days).

The actual measured value may differ by ± 20 per cent from the values obtained from the equation above.

Factor Affecting Modulus of Elasticity of Concrete

The modulus of elasticity of concrete can vary depending on several factors, including the type of concrete mix, the curing conditions, the age of the concrete, and the presence of additives or admixtures.

1. Concrete Mix Proportions:

The ratio of the ingredients in the concrete mix, including the proportion of cement, aggregates, and water, can impact the modulus of elasticity. The concrete prepared with a mix of 1:1:2 will have a higher value of modules of elasticity than a concrete mix of 1:1.5:3.

2. Strength of Concrete:

The modulus of elasticity of concrete tends to increase roughly in proportion to the square root of its strength. For example, M25 concrete exhibits 25,000 MPa and M20 concrete has 22,360 MPa of modulus of elasticity.

3. Type of Aggregates:

As of course aggregate has a higher modulus of elasticity, the concrete will have a higher modulus of elasticity. It is observed that the concrete with a higher amount of aggregate will have greater strength.

4. Curing Conditions:

The curing period, encompassing factors like duration and environmental conditions such as temperature and humidity, influences the strength development of concrete, leading to corresponding effects on its modulus of elasticity. Notably, concrete subjected to moist curing tends to yield superior outcomes compared to concrete cured in a dry environment, as the latter may experience shrinkage and the formation of associated cracks.

Also, read: What Is Concrete Curing?: Different Methods Of Curing.

Water-Cement Ratio:

The water-cement ratio affects the porosity and density of concrete. Higher water-cement ratios generally result in lower modulus of elasticity due to increased porosity.

Also, read: What Is Water-Cement Ratio? | Calculation Of W/C | Value Of W/C

FAQs:

References:

• American Concrete Institute. (2008). Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. Farmington Hills, MI: American Concrete Institute. https://www.concrete.org/Portals/0/Files/PDF/Previews/318-08_preview.pdf
• Dr. Ramchandra. (2013). Reinforced Concrete Structure (limit state design). Rajsons Publications Pvt. ltd. Delhi -110006
• [Solved] Consider the following statements concerning elasticity of c. (2023, August 7). Testbook. https://testbook.com/question-answer/consider-the-following-statements-concerning-elast–5f1c4ac72d4b290d0e7eaefa