When it comes to understanding the mechanical behaviour of materials, including concrete, Poisson’s ratio is a critical parameter that plays a significant role. It is a measure of the lateral or transverse strain that occurs in a material when it is subjected to an axial or longitudinal strain. In the case of concrete, it has important implications for its structural behaviour, including its deformation characteristics, stress distribution, and crack development. In this article, we will delve into the concept of Poisson’s ratio of concrete, its significance, and its practical implications in the field of civil engineering.
What is the Poisson’s Ratio?
Poisson’s ratio, denoted by the Greek letter ν (nu), is defined as the ratio of lateral strain (εlateral) to longitudinal strain (εlongitudinal) when a material is subjected to axial or longitudinal loading. Mathematically, it can be expressed as:
Poisson’s ratio = lateral strain/longitudinal strain
Change in length/ Lateral strain = ΔL/L
Change in diameter/longitudinal strain = ΔD/D
ν = (ΔD/D) / (ΔL/L)
ν = – εlateral / εlongitudinal
It is defined as the negative ratio of the lateral strain to the axial strain when a material is subjected to an axial load. In other words, it measures the change in lateral dimension (thickness or width) of a material when it is subjected to an axial strain (change in length) in the direction of the applied load.
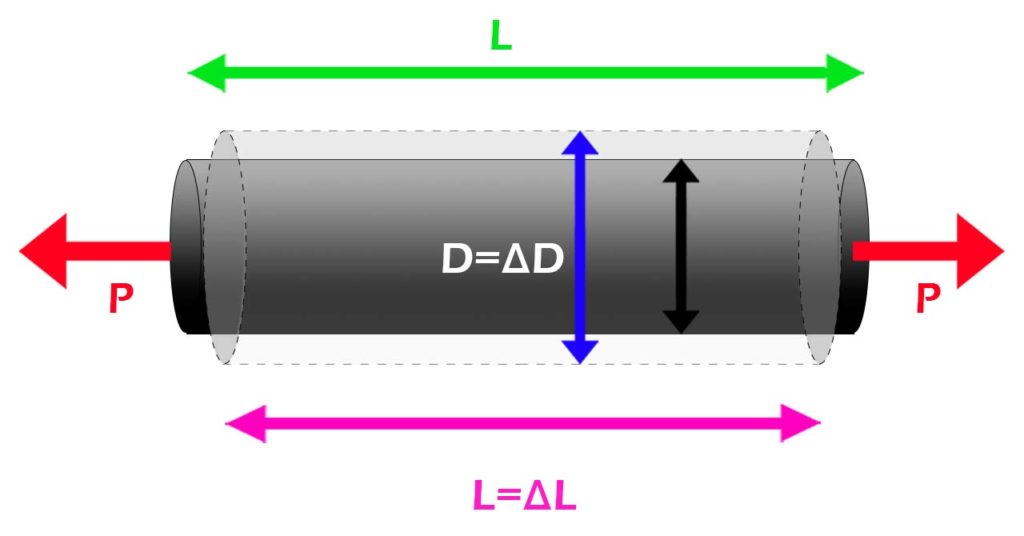
The Poisson’s ratio is a dimensionless quantity that ranges between -1 and 0.5, where -1 represents complete transverse expansion with no axial strain, and 0.5 represents complete incompressibility with no lateral strain.
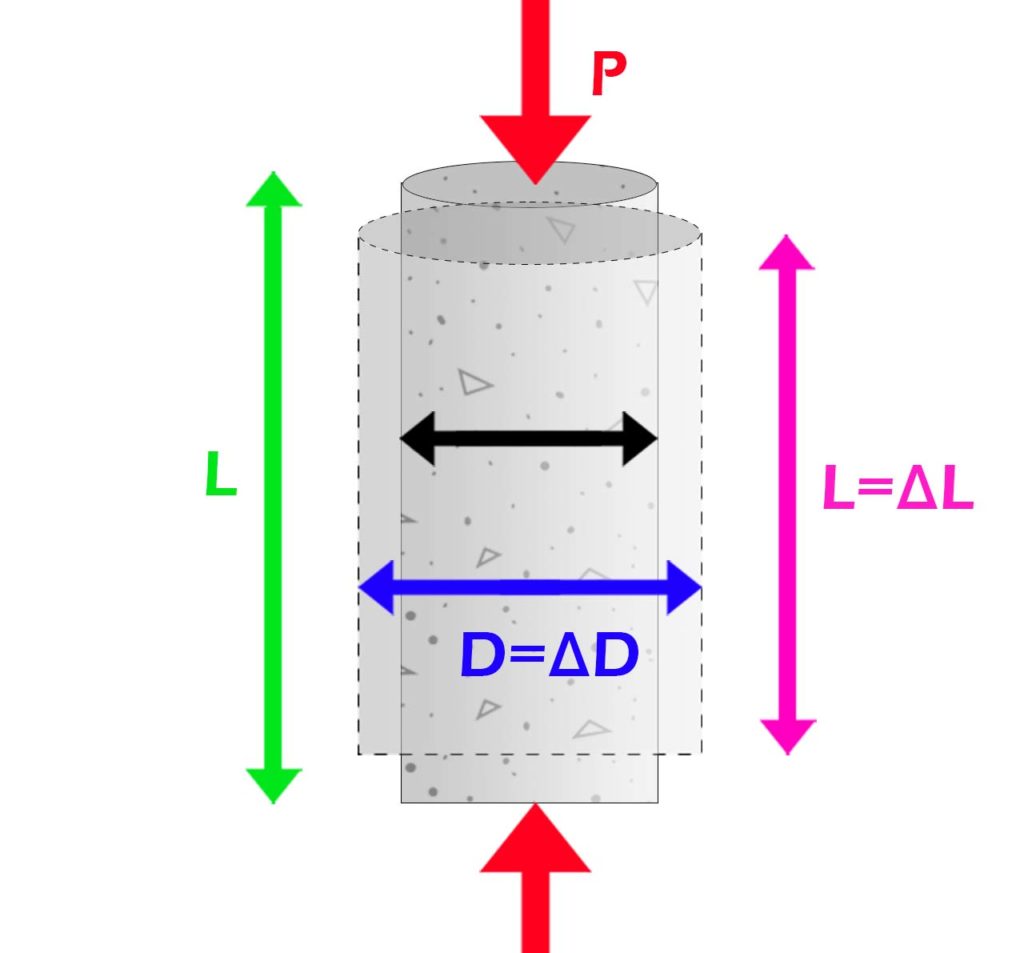
What is Poisson’s Ratio of Concrete?
In the case of concrete, Poisson’s ratio typically ranges from 0.1 to 0.2. This means that when concrete is subjected to axial or longitudinal compression, it tends to expand laterally or transversely by a small amount, typically around 0.1 to 0.2 times the axial or longitudinal strain. Similarly, when concrete is subjected to axial or longitudinal tension, it tends to contract laterally or transversely by a similar amount.
ν = Longitudinal Strain / Lateral Strain
Understanding the Poisson’s Ratio of Concrete
Concrete, like other materials, undergoes deformation when subjected to external loads. When a load is applied to a concrete specimen, it undergoes axial deformation (change in length) in the direction of the applied load, as well as lateral deformation (change in width or thickness) perpendicular to the applied load. The Poisson’s ratio of concrete relates these two types of deformation and provides insights into the material’s behaviour.
The Poisson’s ratio of concrete typically ranges from 0.1 to 0.2, although it can vary depending on various factors, including the type and proportion of materials used in the mix, curing conditions, and the age of the concrete. Generally, concrete has a Poisson’s ratio close to 0.15, which means that it undergoes relatively small lateral deformation compared to its axial deformation.
Significance of Poisson’s Ratio in Concrete
The Poisson’s ratio of concrete has several important implications in civil engineering and construction practices:
Shear Deformation: The Poisson’s ratio affects the distribution of strains within a concrete element subjected to external loads. When concrete undergoes axial deformation, it tends to expand laterally in the perpendicular direction due to Poisson’s effect. This lateral expansion results in shear deformation and affects the overall behaviour of the structure, especially in elements subjected to bending, such as beams and slabs.
Control of Cracking: It also influences the formation and propagation of cracks in concrete structures. Concrete has low tensile strength and is prone to cracking when subjected to tensile stresses. The Poisson’s ratio affects the magnitude and orientation of tensile stresses within a structure, which can influence the crack pattern and propagation.
Load Transfer: The Poisson’s ratio of concrete is also important in load transfer mechanisms between different elements of a structure. For example, in a composite structure such as a pre-stressed concrete beam, it affects the transfer of loads between the pre-stressed tendons and the concrete, influencing the overall structural behaviour.
Material Characterization: The Poisson’s ratio is a crucial parameter in material characterization tests, such as triaxial and consolidation tests, which are commonly performed to determine the mechanical properties of concrete. Accurate determination of the Poisson’s ratio is important for the proper analysis and design of concrete structures.
Impacts of Poisson’s Ratio on Concrete Design
It has a significant impact on the design of concrete structures. Let’s explore some of the key implications of Poisson’s ratio in concrete design:
Deformation Characteristics: Poisson’s ratio affects the deformation characteristics of concrete. When concrete is subjected to axial or longitudinal loading, Poisson’s effect causes it to expand laterally under compression and contract laterally under tension. This differential lateral movement can result in the development of cracks, especially on the tension side of a structure. Therefore, engineers need to account for Poisson’s ratio in the design of concrete structures to ensure that the expected deformations and crack patterns are considered, and appropriate measures are taken to control cracks and prevent a potential failure.
Stress Distribution: Poisson’s ratio affects the stress distribution in concrete elements. The stress concentrations caused by Poisson’s effect can influence the overall behaviour and durability of a structure. For example, in a reinforced concrete beam subjected to bending, the stress concentrations at the corners or edges of the beam due to Poisson’s effect can impact the formation of cracks and affect the overall strength and performance of the beam. Proper consideration of Poisson’s ratio is important in the analysis and design of concrete structures to accurately predict stress distributions and ensure the structural integrity of the elements.
Shear Behavior: Poisson’s ratio also affects the shear behaviour of concrete. Shear strength is an important parameter in the design of structural elements such as beams, slabs, and foundations. Poisson’s ratio can influence the shear transfer between different parts of a structure and affect its shear capacity. Therefore, understanding the effects of Poisson’s ratio on shear behaviour is crucial in designing safe and efficient concrete structures, and appropriate shear reinforcement detailing may be required to account for its effects of it.
Dynamic Analysis: Poisson’s ratio holds significant importance in the realm of dynamic analysis and design, especially in seismic applications. It affects the propagation of stress waves in concrete and impacts the response of concrete structures to seismic loads. Accurately determining is crucial in dynamic analysis to effectively capture the dynamic behaviour of concrete structures and ensure their performance during seismic events.
Material Properties: Poisson’s ratio is an inherent material property of concrete, and its value can vary depending on factors such as the type of aggregate, water-cement ratio, and curing conditions. Therefore, the consideration of Poisson’s ratio is essential in the selection of concrete mix proportions and materials to achieve the desired performance and behaviour of a structure. Accurate determination of Poisson’s ratio for the specific concrete mix being used is important in designing structures with optimal performance.
FAQs:
Q: What is the Poisson’s ratio of Concrete?
A: The Poisson’s ratio of concrete ranges from 0.1 to 0.2. This means that when concrete is subjected to axial or longitudinal compression/tension, it tends to expand/contract laterally or transversely by a small amount, typically around 0.1 to 0.2 times the axial or longitudinal strain.
Q: How is Poisson’s ratio of concrete determined?
A: Poisson’s ratio of concrete is typically determined through experimental testing. Lateral strain and axial strain measurements are obtained from tests, such as uniaxial compression tests or flexural tests, and then the ratio of lateral strain to axial strain is calculated to determine Poisson’s ratio.
Q: Why is Poisson’s ratio important in concrete?
A: Poisson’s ratio is important in concrete because it influences the propagation of stress waves and affects the response of concrete structures to dynamic loads, such as seismic loads. It is a critical parameter in the dynamic analysis and design of concrete structures to accurately capture their dynamic behaviour and ensure their seismic performance.
Q: How does Poisson’s ratio of concrete affect seismic performance?
A: Poisson’s ratio of concrete can affect the behaviour of concrete structures under seismic loads. Higher values of Poisson’s ratio can result in increased deformation and reduced stiffness of the concrete, potentially leading to reduced seismic performance. Accurate determination of Poisson’s ratio is important in seismic design to properly capture the dynamic response of concrete structures and ensure their performance during earthquakes.
Also read:
![]()







