The slenderness ratio plays a pivotal role in assessing the stability of columns and other structural elements. This ratio provides valuable insights into the potential for buckling, a critical consideration in the design and safety of structures.
Slenderness Ratio Of Compression Members
The slenderness ratio of compression members is a dimensionless parameter calculated as the ratio of the effective length of a structural member to its least radius of gyration. It is defined as the ratio of unsupported length (\( L \)) of the compression member, to the appropriate least radius of gyration (\( r \)) of the compression member and denoted by \( \lambda \). The formula to calculate the slenderness ratio is given,
\( \lambda=K\frac Lr \)
Where:
- \( \lambda \) is the slenderness ratio of compression members,
- \( k \) is the constant
- \( L \) is the effective length of compression members,
- \( r \) is the least radius of gyration of the compression members’ cross-sectional area.

Effective Length (\( l \)) of Compression Member
The effective length of a compression depends upon end restraint conditions. The end restraint conditions are of two types, viz., (i) position restraint and (ii) direction restraint.
- Position restraint.
In position restraint, the end of a column is not free to change its position but rotation about the end of a column may take place, e.g., the hinged end of a column as shown in
- Direction restraint.
In direction restraint, the end of the column is free to change its position but rotation at the end of the column cannot take place.
When any end of a column has restraint in position and direction, then the end is not free to change its position, and the rotation about the end of the column also cannot take place.
There are various combinations of restraints on either or both axes. The restraint conditions at the two ends of a column may be different or maybe the same. Following are the ideal cases of the end conditions:
The effective length of compression members as per IS: 456–2000 of Table 28 is,
| S.No. | Degree of End Restraint of Compression Members | Symbol | Theoretical | Recommended |
|---|---|---|---|---|
| 1. | Effectively held in position and restrained against rotation in both case | 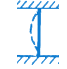 | 0.50 \( l \) | 0.65 \( l \) |
| 2. | Effectively held in position at both ends, restrained against rotation at one end |  | 0.70 \( l \) | 0.80 \( l \) |
| 3. | Effectively held in position at both ends, but not restrained against rotation | 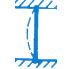 | 1.00 \( l \) | 1.00 \( l \) |
| 4. | Effectively held in position and restrained against rotation at one end, and at the other restrained against rotation but not held in position |  | 1.00 \( l \) | 1.20 \( l \) |
| 5. | Effectively held in position and restrained against rotation in one end, and at the other partially restrained against rotation but not held in position |  | – | 1.00 \( l \) |
| 6. | Effectively held in position at one end but not restrained against rotation, and at the other end restrained against rotation but not held in position |  | 2.00 \( l \) | 2.00 \( l \) |
| 7. | Effectively held in position and restrained against rotation at one end but not held in position nor restrained against rotation at the other end |  | 2.00 \( l \) | 2.00 \( l \) |
In the above table “\( l \)“ is the unsupported effective length of compression members or columns.
Effective Length Factor (\( k \))
The effective length factor (\( k \)) is a parameter that accounts for the end restraint (support) and lateral bracing conditions of a column. It serves as a modifier to the actual length of the column, adjusting it to represent the influence of the specific end conditions on the column’s stability. The choice of (\( k \)) reflects whether the ends of the column are pinned (free to rotate), fixed (completely restrained against rotation), or exhibit other types of support and bracing.
The effective length factor is used in the calculation of the effective length, contributing to a more accurate assessment of the column’s behaviour under various loading and stability conditions in structural analysis and design.
The formula for determining the effective length (\( L_e \)) of a column based on the actual length (\( L \)) and the effective length factor (\( k \)) is given by:
$$ L_{e}\;\;=k⋅L $$
Here:
- \( L_e \) is the effective length of the column,
- \( L \) is the actual length of the column,
- \( k \) is the effective length factor.
Radius Of Gyration (\( r \))
The radius of gyration is a geometric property of a structural section that quantifies how the cross-sectional area is distributed about a particular axis. It is often denoted by the symbol “\( r \)” and is a critical parameter in structural engineering calculations, particularly when analyzing the stability of columns.
Mathematically, the radius of gyration (\( r \)) is defined as the square root of the ratio of the moment of inertia (\( I \)) to the cross-sectional area (\( A \)):
$$ r\;=\;\sqrt{\frac IA} $$
In this formula:
- \( r \) is the radius of gyration,
- \( I \) is the moment of inertia of the section,
- \( A \) is the cross-sectional area.
The moment of inertia is a measure of an object’s resistance to changes in its shape about a particular axis. The radius of gyration provides a convenient way to express this property by representing the distribution of the area in a single value. A smaller radius of gyration indicates that more of the material is located closer to the axis of rotation, while a larger radius of gyration suggests that the material is more dispersed from the axis.
Relationship Between Slenderness and Buckling
Euler’s critical buckling load formula explains the relationship between slenderness and buckling which is applicable to both long and slender columns: According to the Euler formula, the slenderness ratio exhibits an inverse relationship with the radius of gyration. In simpler terms, the tendency of buckling failure is highest when the radius of gyration (\( r \)) is at its minimum.
\( P_{critical}={\frac{\pi^2.E.I}{\left(k.L\right)^2}}_{}\;\;\;\; \)
where:
- \( P_{critical} \)is the critical buckling load,
- \( E \) is the modulus of elasticity of the material,
- \( I \) is the moment of inertia of the cross-sectional shape,
- \( k \) is the column effective length factor,
- \( L \) is the effective length of the column.
The slenderness ratio (\( L \)) appears in the denominator of the critical buckling load formula, indicating an inverse relationship. This means that as the slenderness ratio increases, the critical buckling load decreases, making the column more susceptible to buckling.
The critical buckling load is the maximum axial load that a slender column can carry without undergoing buckling. When the applied load exceeds this critical load, the column may buckle, leading to instability.
Also, read: Modulus Of Elasticity Of Concrete
Types of Columns Based on Slenderness Ratio:
Short Columns:
When the slenderness ratios (\( \lambda \)) are less than 12, then the columns and compression members are called as short columns. Behaviour is dominated by material strength rather than geometric considerations.
\(\lambda\;=\;\frac{l_{ex}}D\;or\;\frac{l_{ey}}b\;<\;12\)
where:
- \( D \) is the depth of the column with respect to the major axis and \( b \) is the width of the column.
- \( l_{ex} \) and \( l_{ey} \) are the effective lengths of the column with respect to the major and the minor axes respectively
Long (slender) Columns:
When either of the slenderness ratios exceeds 12, then the columns and the compression members are called long (slender) columns. The load-carrying capacity of a long column is influenced by the slenderness effect. The slenderness effect produces additional bending moments because of transverse deformations. The long columns may fail either due to failure of materials or by buckling.
\(\lambda\;=\;\frac{l_{ex}}D\;or\;\frac{l_{ey}}b\;>\;12\)
where:
- \( D \) is the depth of the column with respect to the major axis and \( b \) is the width of the column.
- \( l_{ex} \) and \( l_{ey} \) are the effective lengths of the column with respect to the major and the minor axes respectively
Also, read: Column Failure: Causes | Types | Prevention
FAQs:
Q: What is the effective length factor (k)?
Answer: The effective length factor (\( k \)) is a dimensionless parameter used to modify the actual length of a column based on its end support conditions.
Q: How does the effective length factor affect the design of columns?
Answer: The effective length factor accounts for end restraints and lateral bracing conditions, influencing the effective length used in the calculation of the slenderness ratio and, consequently, the stability of the column.
Q: What is the radius of gyration?
Answer: The radius of gyration (\( r \)) is a measure of how the cross-sectional area of a structural member is distributed about its centroidal axis. It is calculated as, $$ r\;=\;\sqrt{\frac IA} $$ where: (\( I \)) is the moment of inertia and (\( A \)) is the cross-sectional area.
Q: How does the radius of gyration influence the stability of columns?
Answer: A smaller radius of gyration implies a more concentrated distribution of material, making the column less prone to buckling. It is a key parameter in the calculation of the slenderness ratio.
References:
- Dr. Ramchandra. (2013). Reinforced Concrete Structure (limit state design). Rajsons Publications Pvt. ltd. Delhi -110006. Limit State Theory and Design of Reinforced Concrete – Dr. Ramchandra – Google Books
- Bhavikatti,. S.S. (2016). Design of RCC Structural Elements (RCC Vol-1) (2nd Ed.). New Age International Publication. Design Of R.C.C. Structural Elements Vol. I – Google Books
![]()







