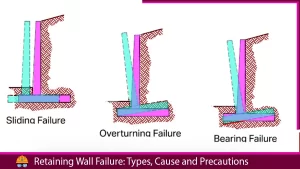
Accurately estimating lateral earth pressure is crucial in designing structures like earth-retaining walls, bridge abutments, basement structures, sheet piles, and trenches. This article introduces the timeless theories of Coulomb and Rankine regarding lateral earth pressure and explores their practical application in engineering. Lateral earth pressure is a critical concept in civil engineering, influencing the stability and safety of structures interacting with soil. This article delves into the fundamentals of earth pressure, its types, and its significance in various civil engineering projects.
Types of Earth Pressure:
In geotechnical engineering, earth pressure is classified into three categories.
- Lateral Earth Pressure
- Vertical Earth Pressure
- Horizontal Earth Pressure
What is Lateral Earth Pressure?
Lateral earth pressure refers to the pressure exerted by soil against a retaining structure, such as a wall or a basement. This pressure is caused by the weight of the soil and any additional external loads acting on it.
When designing structures that interact with soil, such as retaining walls or sheet pile walls, it is crucial to consider the lateral earth pressure. Failure to account for this pressure can result in structural instability and potential collapse.
Types Of Lateral Earth Pressure
There are three main types of lateral earth pressure: active, passive, and at rest.
- Earth Pressure at Rest: This pressure occurs when there is no movement or change in stress within the soil mass.
- Active Earth Pressure: This occurs when the soil is in a loose state and tends to push the retaining structure away.
- Passive Earth Pressure: On the other hand, arises when the soil is dense and resists movement, exerting pressure towards the structure.
Plastic Equilibrium in Soil
Plastic equilibrium is attributed to a soil mass when every point within it is on the brink of failure. Rankine examined the stress conditions associated with states of plastic equilibrium that can occur uniformly across a semi-infinite soil mass affected solely by gravity, without any additional external forces. The stress conditions during plastic equilibrium can be expressed by the following Mohr-Coulomb equation:
\( \frac{\sigma_1-\sigma_3}2-\frac{\sigma_1+\sigma_3}2=\sin\phi=c.\cos\phi \)
\( \sigma_1 \) and \( \sigma_3 \) = major and minor principal stresses at any point in the soil mass, at failure.
The calculation of stress in a condition of plastic equilibrium relies on the theory known as plasticity. The soil-specific aspect of plasticity theory is grounded in Mohr’s theory of rupture. When the material is on the verge of plastic flow, it remains in static equilibrium, adhering to the equilibrium equations in the x-z plane.
The combination of equations 20.4, 20.5, and 20.6 results in an equation known as Kotter’s equation. Solving this equation, given specific boundary conditions, provides the orientation of slip lines along with the stress at each point within the failure zone (Sokolovsky, 1965).
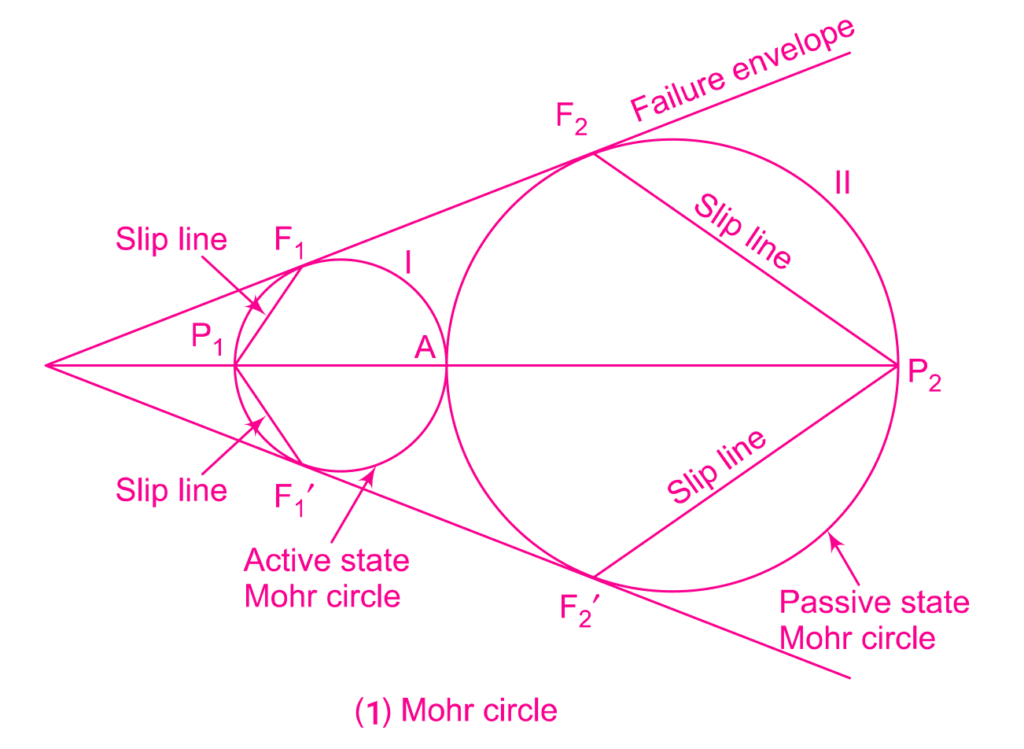
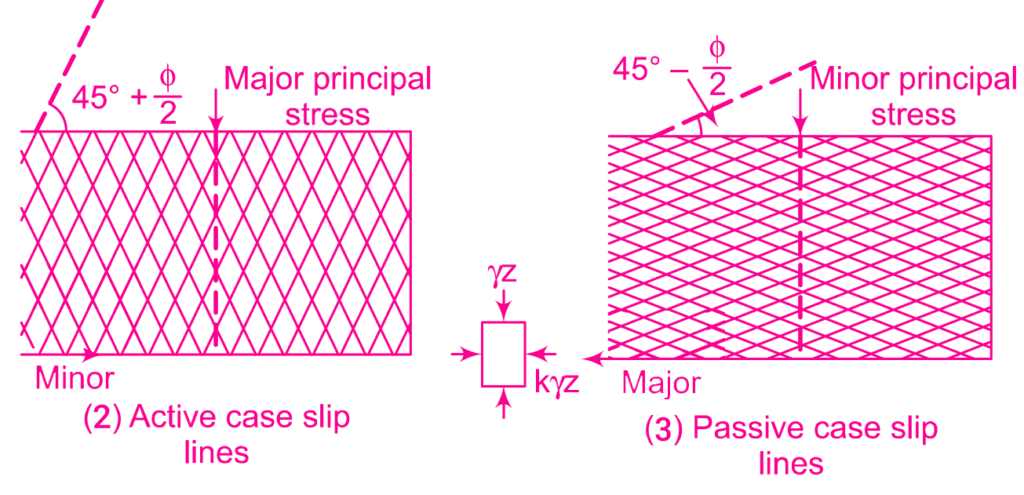
Figure a, illustrates the conditions of active and passive plastic equilibrium in non-cohesive soil on a horizontal ground surface. In the active state, the major principal stress \( \sigma_1 \) is vertical, and the minor principal stress \( \sigma_3 \) is horizontal, represented by Circle I. Point A corresponds to the major principal stress, and poles \( P_1 \) and \( P′_1 \) represent the minor principal stress (i.e., horizontal stress or lateral pressure). The circle touches the failure envelopes at\( F_1 \) and \( F’_1 \), and lines \( P_1F_1 \) and \( P_1 F’_1 \) indicate the directions of failure planes or slip lines. These slip lines are also depicted in Fig. a (2).
Similarly, in the passive state, the minor principal stress is vertical, and the major principal stress is horizontal, represented by Circle II. Pole \( P_2 \) corresponds to the major principal stress, and the circle touches the failure envelope at \( F_2 \) and \( F’_2 \). Lines \( P_2F_2 \) and \( P_2 F’_2 \) indicate the directions of slip lines for the passive case.
The ratio of the horizontal stress \( \sigma_h \) to the vertical stress \( \sigma_v \) is called the coefficient of earth pressure K. \( \sigma_1 \) = \( \sigma_v \) and \( \sigma_3 \) = \( \sigma_h \) when soil is the active state of plastic equilibrium.
\( \frac{\sigma_h}{\sigma_v}=K_a \)
\( K_a=\frac{\sigma_v}{\sigma_h}=\frac1{\tan^2\left(45^\circ+{\displaystyle\frac\phi2}\right)}=\cot^2\left(45^\circ+\frac\phi2\right)=\frac{1-\sin\left(\phi\right)}{1+\sin\left(\phi\right)} \)
where, \( K_a \) = co-efficient of active earth pressure.
Similarly, in a passive state, \( \sigma_1 \) = \( \sigma_h \) and \( \sigma_3 \) = \( \sigma_v \)
\( K_p=\frac{\sigma_h}{\sigma_v}=\tan^2\left(45^\circ+\frac\phi2\right)=\frac{1+\sin\left(\phi\right)}{1-\sin\left(\phi\right)} \)
where, \( K_p \) = co-efficient of passive earth pressure.
When the soil is in the elastic equilibrium the ratio of horizontal to vertical stress is called co-efficient of earth pressure of rest.
\( \frac{\sigma_h}{\sigma_v}=K_0 \)
where, \( K_0 \) = co-efficient of earth pressure at rest.
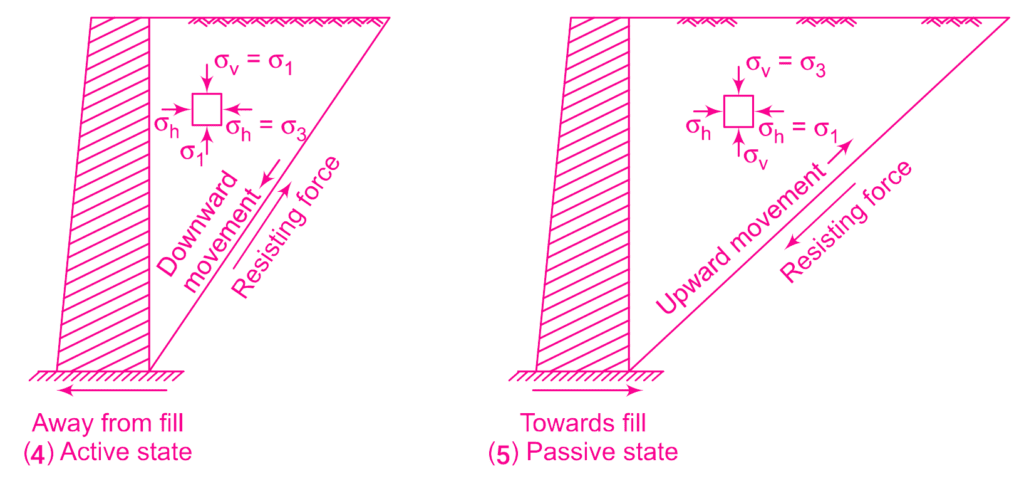
The active and passive states of plastic equilibrium behind a retaining wall are shown in Figure B. In the active state, the wall moves away from the backfill, causing a section of the backfill right behind the wall to separate from the rest of the soil. This separated wedge, moving with the wall, is known as the failure wedge. The resistance force, generated by the shear strength of the soil, acts upward along the failure plane (slip lines). Figure B (5) shows the passive case in which the wall moves towards the fill because of thrust.
Earth Pressure at Rest
The calculation of the earth pressure at rest applied to the rear of a rigid and unyielding retaining structure involves the application of elasticity theory. This assumes the soil to be semi-infinite, homogeneous, elastic, and isotropic. If we examine a soil element at a depth z subjected to vertical stress \(( \sigma_v \)) and horizontal stress \(( \sigma_h \)):, with no shear stress present, the lateral strain \( \varepsilon_h \) in the horizontal direction can be expressed as follows:
\( \varepsilon_h=\frac1E\left[\sigma_h-\mu\left({\sigma_h+\sigma}_v\right)\right] \)
The earth pressure at rest corresponds to the condition of zero lateral strain \( \varepsilon=0 \). Hence,
\( \sigma_h=\mu\left(\sigma_h+\sigma_v\right) \)
or
\( K_0=\frac\mu{1-\mu} \)
where \( K_0 \) is the coefficient of the earth pressure at rest.
The later earth pressure at rest can be expressed by substituting \( P_0 \) to the \( \sigma_h \) and \( \sigma_v \) by \( \gamma.z \)
\( P_0=K_0.\gamma.z \)
The total pressure \( P_0 \) per unit length for the vertical height \( H \) is given by:
\( P_0=\int_0^HK_0.\gamma.z.dz \)
or
\( P_0=\frac12K_0.\gamma.H^2 \)
The behaviour of soil is not in accordance with the elastic theory and does not have a well-defined value of the Poisson’s ratio. The table below gives some value of \( K_0 \) available from experience.
| Soil Type | \( K_0 \) |
|---|---|
| Loose sand | 0.4 |
| Dense sand | 0.6 |
| Sand compacted in layer | 0.8 |
| Soft clay | 0.6 |
| Hard clay | 0.5 |
\( K_0 \) may also be computed from the equation given by Jaky (1944).
\( K_0=1-\sin\left(\phi\right) \)
Earth pressure at rest \(( P_0 \)) is always greater than active earth pressure \(( P_a \)) but less than passive earth pressure \(( P_p \)).
Theories And Methods On Earth Pressure
To calculate the lateral earth pressure, various theories and methods, such as Rankine’s theory, Coulomb’s theory, and the Mononobe-Okabe method are adopted. These methods consider factors such as soil properties, wall geometry, and surcharge loads to determine the magnitude and distribution of lateral pressure.
In addition to design considerations, understanding lateral earth pressure is also important for slope stability analysis. The pressure exerted by soil against a slope can cause it to fail and potentially lead to landslides. Analyzing the lateral earth pressure allows for the assessment of slope stability and the implementation of necessary measures to prevent failures.
rankine’s theory of earth pressure
Active earth pressure occurs when the soil is in a state of failure and is trying to move away from the wall. It is typically considered when the wall moves away from the soil. The active earth pressure is further divided into two cases: active earth pressure at rest and active earth pressure during movement.
Passive earth pressure, on the other hand, occurs when the soil is in a state of failure and is trying to move towards the wall. It is typically considered when the wall moves towards the soil. The passive earth pressure is also divided into two cases: passive earth pressure at rest and passive earth pressure during movement.
Rankine’s theory makes certain assumptions. It assumes that the soil behaves as a homogeneous and isotropic material and that it follows Coulomb’s friction law. The theory also assumes that the soil has a horizontal surface and that there are no external loads acting on the soil.
The theory suggests that the lateral earth pressure acting on a retaining wall can be divided into two components: Active earth pressure and Passive earth pressure.
Active Earth Pressure For Cohesionless Soils:
Active earth pressure is a type of lateral earth pressure exerted by the soil against a retaining wall when the soil is pushing the wall away.
In the case of active pressure, the structure tends to move away from the soil, causing strains in the soil mass, which in turn, mobilise shearing stresses; these stresses help to support the soil mass and thus tend to reduce the pressure exerted by the soil against the structure.
It is often calculated using Rankine’s Earth Pressure theory. The formula for active earth pressure per unit length of wall is given by:
\( P_a=\frac12.K_a.\gamma.H^2 \) …
Where:
- \( P_a \) is the active earth pressure (force per unit length of the wall),
- \( K_a \) is the coefficient of active earth pressure,
- \( \gamma \) is the unit weight of the soil,
- \( H \) is the height of the retained soil.
The coefficient \( K_a \) is related to the angle of internal friction \( \phi \) of the soil for cohesionless soils (no cohesion) and is given by:
\( K_a=\frac{1-\sin\left(\phi\right)}{1+\sin\left(\phi\right)} \) …
Passive Earth Pressure For Cohesionless Soils:
The pressure exerted by the soil on a retaining wall when the wall is pushing the soil.
The formula for passive earth pressure \( P_p \)can be expressed as:
\( P_p=\frac12.K_p.\gamma.H^2 \) …
where:
- \( P_p \) is the passive earth pressure (force per unit length of the wall),
- \( K_p \) is the coefficient of passive earth pressure,
- \( \gamma \) is the unit weight of the soil,
- \( H \) is the height of the retained soil.
The coefficient \( K_p \) is related to the angle of internal friction \( \phi \) of the soil for cohesionless soils (no cohesion) and is given by:
\( K_p=\frac{1+\sin\left(\phi\right)}{1-\sin\left(\phi\right)} \) …
Similar to active earth pressure, passive earth pressure is associated with the soil pushing against a retaining wall. The coefficient \( K_p \) takes into account the natural angle of repose of the soil and is a key factor in determining the magnitude of the passive earth pressure. It’s important to consider these factors in the design and analysis of retaining walls and other structures interacting with soil to ensure stability and safety.
At-Rest Earth Pressure: The pressure exerted by the soil on a retaining wall in a state of equilibrium, neither pushing nor pulling.
Cohesive Soils
Rankine’s Earth Pressure theory can also be applied to cohesive soils, which are soils that contain clay particles and exhibit cohesion in addition to friction. The theory assumes that the soil is cohesion-dominated and does not consider friction along the back of the wall. Similar to the analysis for cohesionless soils, Rankine’s theory for cohesive soils involves determining the active and passive earth pressures.
Active Earth Pressure For Cohesive Soils:
The active earth pressure is the lateral pressure exerted by cohesive soil when the retaining wall tends to move away from the soil. It represents the maximum pressure that the soil can exert on the wall. The formula for passive earth pressure per unit length of wall is as same as active earth pressure for cohesionless soils (see equation 1)
The active earth pressure coefficient \( K_a \) for cohesive soils is determined by the ratio of the cohesion \( c \) to the effective vertical stress \(( \sigma_v \)):
\( K_a=1-\frac{\sigma_c}{\sigma_v} \) …
where, \( \sigma_c \) is the effective cohesion.
Passive Earth Pressure For Cohesive Soils:
Passive earth pressure is the lateral pressure exerted by cohesive soil when the retaining wall tends to move toward the soil. It represents the maximum resistance that the soil can offer against the movement of the wall. The formula for passive earth pressure per unit length of wall is as same as passive earth pressure for cohesionless soils (see equation 3)
The passive earth pressure coefficient \( K_p \) for cohesive soils is determined by the ratio of the cohesion \( c \) to the effective vertical stress \(( \sigma_v \)):
\( K_p=1+\frac{\sigma_c}{\sigma_v} \) …
Here, \( \sigma_c \) is the effective cohesion, and \( \sigma_v \) is the effective vertical stress.
Also, read: Various Types Of Retaining Walls: A Comprehensive Guide 101
FAQs:
Q: What is lateral earth pressure?
Answer: Lateral earth pressure refers to the pressure exerted by soil against a retaining structure, such as a wall or a basement. This pressure is caused by the weight of the soil and any additional external loads acting on it.
Q: What are the types of lateral earth pressure?
Answer: Lateral earth pressures are of three types,
1. Active Earth Pressure: This occurs when the soil is in a loose state and tends to push the retaining structure away.
2. Passive Earth Pressure: In this state, arises when the soil is dense and resists movement, exerting pressure towards the structure.
3. At-Rest Earth Pressure: This pressure occurs when there is no movement or change in stress within the soil mass.
References:
- Punmia, B. C., & Jain, A. K. (2005). Soil mechanics and foundations (17th ed.). Laxmi Publications (P) Ltd. https://www.laxmipublications.com/servlet/lpdispinfo?offset=0&text1=SOIL+MECHANICS+AND+FOUNDATIONS&searchtype=Keywords
- Dr. Ramchandra. (2013). Reinforced Concrete Structure (limit state design). Rajsons Publications Pvt. ltd. Delhi -110006. Limit State Theory and Design of Reinforced Concrete – Dr. Ramchandra – Google Books
- Ishibashi, I., & Hazarika, H. (2015). Soil Mechanics Fundamentals and Applications. CRC Press.
- Verruijt, A. (2018). An introduction to soil mechanics. In Theory and applications of transport in porous media. https://doi.org/10.1007/978-3-319-61185-3
- Ranjan, G., & Rao, A. S. R. (2007). Basic and applied soil mechanics. New Age International.
- Hettler, A., & Kurrer, K. (2020). Earth pressure. John Wiley & Sons.
![]()