Measuring Tape
A measuring tape is a flexible length measuring device which may or may not be encased and used in various applications such as construction, engineering, woodworking, and sewing work. It typically consists of a ribbon or tape of cloth, plastic, or metal that can be wound into a coil, housed in a compact case, and extended to measure lengths. The tape is marked with precise and evenly spaced graduations or markings that allow for accurate measurements to be taken quickly and easily. Measuring tapes are available in various lengths, widths, and measurement systems, and can be used for both short and long-distance measurements.

- Direct method using a tape or wire
- Tacheometric method or optical method
- EDM (Electromagnetic Distance Measuring equipment) method.
Direct Method Using A Measuring Tape
The method of distance measurement involves the use of measuring tape (steel tapes) or wires to attain high accuracy. Although EDM is now the preferred method for precision measurements, steel tape remains useful for measuring shorter distances for setting out purposes.

Correction for Measuring Tape Measurement
Correction for measuring tape measurement refers to the adjustments or corrections applied to the measured length obtained from a measuring tape, to account for various factors that can affect its accuracy. Such factors can include the tape’s stretching or shrinking over time, temperature, tension, and manufacturing defects. To obtain an accurate measurement, it is crucial to correct these factors using appropriate correction formulas or charts.
The correction factors can be positive or negative, depending on the deviation from the standard conditions. Accurately correcting tape measurements can help ensure precise and reliable measurements in construction, surveying, and engineering. Therefore, measurements with measuring tape require correction factors to be applied based on the measurement conditions, as discussed below.
Correction for Absolute Length
Manufacturing defects can cause the actual length of a measuring tape to differ from its designated or nominal length, and over time, the tape may stretch, leading to a change in length. Therefore, it is essential to periodically check the tape’s absolute length under standard conditions. The correction or standardization factor for the absolute length can be determined by:

where
c = the correction per tape length,
l = the designated or nominal length of the tape, and
L= the measured length of the line.
If the absolute length is more than the nominal length the sign of the correction is positive and vice versa.
Correction for Temperature
If the tape is used at a field temperature different from the standardization temperature then the temperature correction to the measured length is
\( C_t=\frac{\alpha\left(t_m-t_0\right)}L \)
where
α = the coefficient of thermal expansion of the tape material,
tm = the mean field temperature, and
t0 = the standardization temperature.
The sign of the correction takes the sign of (tm– t0 ).
Correction for Pull or Tension
If the pull applied to the tape in the field is different from the standardization pull, the pull correction is to be applied to the measured length. This correction is
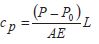
where
P = the pull applied during the measurement,
P0 = the standardization pull,
A = the area of cross-section of the tape, and
E = Young’s modulus for the tape material.
The sign of the correction is the same as that of ( P − P0)
Correction for Sag
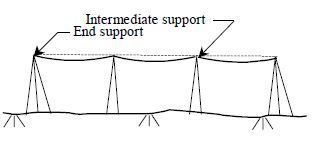
For very accurate measurements the tape can be allowed to hang in a catenary between two supports (Fig. 1a). In the case of long tape, intermediate supports as shown in Fig. 1b, can be used to reduce the magnitude of the correction.
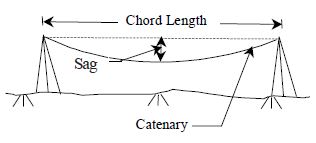
The tape hanging between two supports, free of the ground, sags under its own weight, with maximum dip occurring at the middle of the tape. This necessitates a correction for sag if the tape has been standardized on the flat, to reduce the curved length to the chord length. The correction for the sag is
\( C_g=\frac1{24}\left(\frac WP\right)^2L \)
where
W = the weight of the tape per span length.
The sign of this correction is always negative. If both ends of the tape are not at the same level, a further correction due to slope is required. It is given by
C’g = Cgcosα
where
α = the angle of slope between the end supports.
Correction for Slope
If the length L is measured on the slope as shown in Fig. 2, it must be reduced to its horizontal equivalent L cos θ. The required slope correction is
CS=(1-cosθ)L (exact) ……………(1)
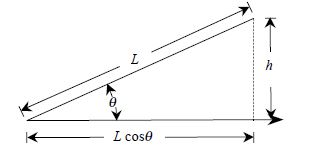
=h2/2L (approximate) ……………(2)
where
θ = the angle of the slope, and
h = the difference in elevation of the ends of the tape.
The sign of this correction is always negative.
Correction for Alignment
If the intermediate points are not in correct alignment with the ends of the line, a correction for alignment given below is applied to the measured length (Fig. 3).
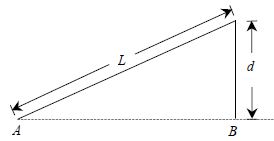
Cm =d2/2L (approximate) ……………(3)
where
d = the distance by which the other end of the tape is out of alignment. The correction for alignment is always negative.
Reduction to Mean Sea Level (M.S.L.)
In the case of long lines in triangulation surveys, the relationship between the length AB measured on the ground and the equivalent length A′B′ at mean sea level has to be considered (Fig. 4). Determination of the equivalent mean sea level length of the measured length is known as a reduction to mean sea level. The reduced length at mean sea level is given by

L’ = R/(R+H) X L ……………(4)
where
R = the mean earth’s radius (6372 km), and
H = the average elevation of the line.
When H is considered small compared to R, the correction to L is given as
The sign of the correction is always negative.
The various tape corrections discussed above, are summarized in Table 1.
Also, read: Dumpy level Surveying | Principal | Components | Application
Error in Correction
Error In Pull Correction Due to Error in Pull
If the nominal applied pull is in error the required correction for the pull will be in error. Let the error in the nominal applied to pull P be ± δP then the
actual pull correction = (P ± δP-P0)/AE x L ……………(5)
and
nominal pull correction = (P – P0)/AE x L ……………(6)
Therefore error = actual pull correction – nominal pull correction
(P ± δP-P0)/AE x L – (P – P0)/AE x L ……………(7)
= ± (L/AB) x δP ……………(8)
From Eq. (6), we have
L/AB = nominal pull correction/ (P-P0)
Therefore from Eq. (8), we get
Error in pull correction = ± nominal pull correction/(P-P0) x δP ……………(9)
From Eq. (9), we find that an increase in pull increases the pull correction.
Error in Sag Correction Due to Error in Pull
If the applied pull is in error the computed sag correction will be in error. Let the error in pull be ± δP then
the actual sag correction
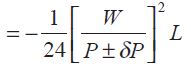
= \( -\frac1{24}\left(\frac WP\right)^2\times L\times\left(1\pm\frac{\delta P}P\right)^{-2} \)
and nominal sag correction
= \( -\frac1{24}\left(\frac WP\right)^2\times L \)
Therefore, error = \( -\frac1{24}\left(\frac WP\right)^2\times L\times\left[\left(1\pm\frac{\delta P}P\right)^2-1\right] \)
= ± nominal sag correction \( \frac{2\delta P}P \) ……………(10)
Eq. (10) shows that an increase in pull correction reduces the sag correction.
| Correction | Sign | Formula |
|---|---|---|
| Absolute length (Ca) | ± | \( \frac ClL \) |
| Temperature (Ct) | ± | \( \alpha\left(t_m-t_0\right)L \) |
| Pull (Cp) | ± | \( \frac{\left(P-P_0\right)}{AE}L \) |
| Sag (Cg) | – | \( \frac1{24}\left(\frac WP\right)^2L \) |
| Slope (Cs) | – | \( \left(1-\cos\left(\theta\right)\right)L \) (exact) |
| Alignment (Cm) | – | \( \frac{h^2}{2L}L \) (approximate) |
| Mean sea level (Cmsl) | – | \( \frac{d^2}{2L}L \) (approximate) |
Also, read: Theodolite Surveying | 2 Types of Adjustments | Errors
![]()







